大老李聊数学

2022年菲尔兹奖得主做了啥——詹姆斯·梅纳德

不久前，四年一度的数学届的最高奖项之一，菲尔兹奖的颁奖结果已经宣布，产生了四位获奖者。有网友想让我介绍一下这四位获奖者的数学上的主要成果，所以我准备就做这样一个系列的节目，给大家介绍下几位获奖者的主要数学成果和一些有趣的生平经历。

（詹姆斯梅纳德的近照，转自Quanta Magazine）

第一篇文章，我就介绍詹姆斯·梅纳德(James Maynard，1987年6月10日－)。梅纳德的主要研究领域是解析数论。解析数论是用各种数学分析的手段研究数论的数学领域。数论就是研究数字性质的理论，而数字的性质最重要的莫过于自然数，自然数中最重要的莫过于质数。一些爱好者熟悉的容易理解，却又非常困难的数学猜想，比如哥德巴赫猜想、孪生素数猜想，乃至黎曼猜想，都属于解析数论中的问题。数论是大家喜闻乐见的领域。但对爱好者来说，这也是一个容易误入歧途的领域，我绝对不建议各位业余爱好者研究以上几个猜想。即使是专业数学研究者，要投身这一领域，也是要冒很大风险的。而梅纳德就选择了这一领域，并且在2013年，其刚取得博士学位不久，就得到了解析数论中的一个大的成果，这个成果是关于孪生素数猜想的。

孪生素数猜想：

那些大小仅相差2的质数对，称为“孪生质数”，比如：3和5，5和7,11和13，10016957和10016959等。

孪生素数猜想是指：存在无穷多对“孪生质数”，这个猜想至今仍未被证明。目前，已证明的最好结论是：

存在无穷多对质数，其大小之差不超过246。

说到2013年和孪生素数猜想，我相信你能想到的一个新闻就是：时年55岁的张益唐证明了存在无穷多个对素数，其间隔小于7000万。因为这是第一次证明存在无穷多对质数，其间隔有一个有限上界，再加上张老此前一直默默无闻，经历也颇具戏剧性，所以张益唐的名字很快上了各大新闻，为大家所熟知。张老的这个发现确实很重大，确实值得一书。

但不为大众所熟知的是，就在张老的论文发表后的半年，梅纳德也发表了一篇关于素数间隔的论文。这篇论文实际上证明了，存在无穷多对质数，间隔小于600，所以他的结果要比张益唐的强。梅纳德的结果甚至更为一般化，他给出了任意连续数量的质数的最小间隔，比如存在无穷多组连续三个、四个、五个质数等等，其中最小的和最大的那个间隔是多少。所以，这是一个相当好的成果。

但问题就在于梅纳德发表论文的时间比张益唐晚了半年，他也只是一名26岁初出茅庐的博士，所以他的这个成果并没有引起什么关注，很多人也只是认为他改进了张益唐的结果。但在数论专家眼里，梅纳德当时的结果是非常出色的。在外人看来，梅纳德在这件事上运气不太好，但这在数学领域中是再正常不过的情况。同一个问题，如果有很多人在研究，那么往往只有第一个解决的人可以得到大部分荣誉。

而梅纳德在这个问题上，他不但与张益唐撞车了，他还与另一位功成名就的数学家撞车了，那就是陶哲轩。

陶哲轩在看到张益唐发表了他的论文之后，对素数最小间距问题产生了很大的兴趣。陶哲轩把这个问题加入了一个一个数学领域的集体合作项目——Polymath，目标是改进张益唐的结果。很快，几乎与梅纳德同时，陶也把最小间距进行了大幅改进到几百的数量级。所以，梅纳德不幸与陶哲轩撞车了。

当陶哲轩得知梅纳德也得到了相同的结果时，表现得非常大度，甚至还有点开心。陶说：“诚实地说，梅纳德的证明比我写得简洁干净，而且他得到了比我略强的结果”。陶哲轩为了避免梅纳德的成果被忽视，选择了不正式发表他的结果，也不与梅纳德共同署名发表论文。因为他知道，如果共同署名，那么多数人会认为他的贡献是主要的，但这不是事实。最终，梅纳德单独就这个成果发表了论文，这是梅纳德的幸运之处。现在我们知道这个质数最小间隔已经被缩小到246。

尽管梅纳德失去了在2013年一举成名的一次机会，但这不影响他对数学的热情和质数的热爱。2014年，梅纳德有发表了一篇有关质数最大间距的问题的论文。我们知道，相邻两个质数之间的间距可以是任意大，这是很容易证明的。但如果问：在多大的自然数范围内，其中一定有一定间隔的质数，这就是质数的大间距问题。梅纳德在2014年，在这个领域，同样给出了一个改进的结果。

质数的大间距问题。2014年，梅纳德证明了，在前x个自然数中，必然存在一对质数，其间隔大于：

$t(1+o(1))\frac{(\log x)(\log \log x)(\log \log \log \log x)}{(\log \log \log x)^{2}}$

其中，t是某个常数。陶哲轩几乎在同一时刻，证明了非常相似的结论。

但这次不幸的是，他又与陶哲轩撞车了。陶哲轩和另两名合作者几乎在同一时间，在这个问题上给出了几乎同样的结果。此后，陶哲轩与梅纳德撞车的事情，在数论圈里成了一个梗。以至于2015年，当陶哲轩证明了“埃尔德什偏差问题”的时候，他从侧面向梅纳德身边的人打听了一下，询问梅纳德是否在证明同样的问题。当他得知否否定的回答后，陶哲轩长出一口气，心说，终于没有撞车了。

埃尔德什偏差问题并不是数论里的一个典型问题，而梅纳德则继续专心在解析数论的领域。2019年，梅纳德解决了有80年历史的一个猜想：达芬——舍费尔猜想（Duffin-Schaeffer conjecture），这个猜想是关于用有理数去近似逼近无理数的。

很早以前的人们就知道用有理数去近似无理数。比如关于 $\pi$ ，祖冲之就给出两个近似值， $\frac{22}{7}$ 和 $\frac{255}{113}$ 。如果问：能否用有理数分数无限的逼近无理数，答案当然是可以。因为你总可以把无理数在某个小数点后截断，然后当成一个有理数并转化成分数。这个分数当然可以任意的接近这个无理数。

但显然，当我们用有理数近似无理数的时候，我们希望这个有理数的分母越小越好。比如 $\frac{355}{113}$ ，约等于3.1415920，那在近似 $\pi$ 这件事情上，它肯定要比分数 $\frac{314159}{100000}$ 好非常多，因为 $\frac{355}{113}$ 用了更小的分母，完成了更高的近似度。

那么，数学家就问了这样一个问题：当寻找无理数的近似分数的时候，近似程度的效率可以达到多大？这里的“效率”的意思就是分母尽可能小，近似程度尽可能高。

关于这个问题，1837年，数学家狄利克雷证明了这样一个结论：当用有理数分数去近似无理数时，总可以找到一个近似分数，如果这个分数的分母是n，则它与这个无理数之间的误差小于 $\frac{1}{n^2}$ 。也就是，当使用分数近似无理数时，它与目标无理数的误差以分母平方的倒数快速逼近。

比如 $\frac{22}{7}$ ，它与 $\pi$ 的误差小于 $\frac{1}{49}$ ， $\frac{355}{113}$ latex 与 $\pi$ 的误差小于 $\frac{1}{113^2}$ 。倒过来考虑也可以，比如，当需要找到一个分数与 $\pi$ 的误差小于一万分之一，那么存在符合这个要求的某个分数，而且分母小于100，因为100的平方是1万。

狄利克雷的这个定理当然非常有用，它说明有理数在近似无理数时，是非常有效率的。但数学家还没完，他们继续发问：如果对近似分数的分母施加限制，结果会如何？比如说，只允许分母取1到9；或者分母的个位数只能是1；或者分母只能是质数等等，加入这些条件后，近似效率会如何？

那么显然，对分母取值范围的限制会限制近似程度。对分母的限制越大，近似程度就会越低。在1941年，两位数学家，达芬和舍费尔对这个问题提出了一个定量化的猜想，讨论对分母的限制程度会如何限制近似程度，这个猜想后来就被称为达芬——舍费尔猜想。

曾经的“达芬—舍费尔猜想”，现在叫“达芬—舍费尔—库库洛普洛斯—梅纳德定理”，它的内容是：

如果函数f为: $\mathbb{N} \rightarrow \mathbb{R}^{+}$ ，那么“几乎”对所有的 $\alpha$ ，以下不等式：

$\left|\alpha-\frac{p}{q}\right|<\frac{f(q)}{q}$

其有无穷多的、互质的整数解p和q时，当且仅当p，q有以下条件：

$\sum_{q=1}^{\infty} f(q) \frac{\varphi(q)}{q}=\infty$ 。

其中的 $\varphi(q)$ 是欧拉 $\varphi$ 函数，意思是小于等于q的自然数中与q互质的整数个数。

“几乎”是一个数学术语，可以简单理解为“例外情况非常少”，例外的情况占总数的比值趋向于0。

如果定义 $f(q)=\frac{1}{q}$ , 又当q为质数时， $\phi(q)=q-1$ ，则：

$\sum_{q=1}^{\infty}f(q)\frac{\varphi(q)}{q}$ $=\sum_{q=1}^{\infty}\frac{1}{q}\frac{q-1}{q}=\sum_{q=1}^{\infty}(\frac{1}{q}-\frac{1}{q^2})$ ，

发散。意味着不等式：

$\left|\alpha-\frac{p}{q}\right|<\frac{f(q)}{q}=\frac{1}{q^2}$ ,有无穷多组解。这就回到了狄利克雷所证明的情况。

近80年后，梅纳德和另一位合作者共同证明了达芬-舍费尔猜想，这是梅纳德的又一项主要数学成果。那么现在达芬-舍费尔猜想应该怎么称呼呢？如果叫“达芬——舍费尔定理”其实不太公平。之前有读者指出，当一个猜想被解决后，应该在后面增加证明者的名字，再改称定理。比如“费马大定理”，应该改称“费马——怀尔斯定理”。这种说法有些道理。那么按照这个原则，“达芬-舍费尔猜想”现在就应该被叫做“达芬-舍费尔-库库洛普洛斯-梅纳德定理”，你能否记住这个名字我就管不着了。

最后，来一个梅纳德证明的，一个非常容易理解，又是非常难以证明的定理。它同样是关于质数的：存在无穷多个质数，它的10进制表示中，没有“7”，而且把数字“7”换成任何0到9中的任何一个数字，此结论都成立。这个结论非常有意思，它也是告诉了我们一些质数的分布规律。

梅纳德证明了，在质数表中，删去所有含有数字“7”的质数，这个质数表仍然可以无限地写下去：

2, 3, 5, 7, 11, 13,17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 …

删除含有0到9的任何一个数字后，仍然有同样的结论。

而且梅纳德是从更大的进制单位开始证明这个结论的。你可以想象，在更大的进制下，单个数字所起的作用就会小许多，这个命题的证明难度也会变小。比如100进制下，每一位有100种取值。去掉其中一种，对整体上可表示的数字范围的影响是非常小的。所以梅纳德就从更大的进制开始，逐步向10进制逼近。

据说，在12进制的情况下，梅纳德卡住了非常长的时间。但他还是坚持了下来，完成了10进制下的证明，他自己对此结果也是非常满意。但目前，没有看到梅纳德继续往9进制以下证明的消息，我们可以简单分析一下，进制单位再缩小会如何。

极端一些，直接从2进制看，显然一个质数不可能都是由0构成。那么是否存在无穷多个由1构成的二进制质数呢？其实全部由1构成的二进制质数，就是梅森质数。是否存在无穷多个梅森质数，目前猜想是真，但至今仍未证明。这个猜想已经存在数百年之久，当然是非常困难的。

关于梅森素数：

容易证明对 $2^n-1$ 形式的数字，仅当n为质数时，其可能为质数。对那些形如 $2^p-1$ 类型的质数，称为“梅森素数”，比如:

$2^2-1=3$ ，

$2^3-1=7$ ，

但：

$M_{11}=2^{11}-1=2047=23 \times 89$ ，不是质数。

至今未能证明：存在无穷多个质数p，使得 $2^p-1$ 是质数，也未能证明：存在无穷多个质数p，使得 $2^p-1$ 是合数。

而所有的的梅森素数，其二进制形态都是若干个1的连写：

111…..111。

3进制会如何呢？感觉上可以存在无穷多个没有数字“0”、”1“或”2”的3进制质数。但同样，要证明此结论是非常困难的。

那么以上简单分析可以看出，梅纳德证明的结论是可以压缩到2进制的。但是个人感觉，进制数再往下的话，问题的难度呈直线上升，以至于梅纳德目前也就停留在十进制的结论下。

好了，以上给大家简单介绍了一下梅纳德的数学成就，可以看出，梅纳德对质数有执着的偏好。众所周知，关于质数的数学命题往往都是非常困难的。梅纳德的博士导师也曾劝梅纳德不要研究那些关于质数的猜想，但梅纳德对质数有执着的偏好和信念，所以仍旧投身了这一研究领域，并且得到了一些杰出的成果。恭喜梅纳德，下期文章再见！

参考链接：

https://www.quantamagazine.org/new-proof-settles-how-to-approximate-numbers-like-pi-20190814/

https://www.quantamagazine.org/number-theorist-james-maynard-wins-the-fields-medal-20220705/

1个球变2个球——巴拿赫塔斯基悖论

这篇知乎上的文章中的后半部分，我们领略了数学家维塔利的一个构造，这个构造可以把一个圆变成两个圆。

回顾一下维塔利的构造要点。首先，这种构造之所以存在，是基于无穷集合的基数理论。无穷集合中，集合的真子集可以与自身建立一一对应，这是这种构造存在的基本理论依据。但是，对不可数集合，要建立某种貌似离散的切割和组合操作，完成子集到自身的一一对应，难度还是很大的。从维塔利的构造中，我们看到了这个构造的基本理念：

把一个不可数集合分割成无数个子集，每个子集都是可数集。可数集中，比较容易建立子集到整体的一一对关系，所以最后的重组工作就比较容易，难点在于分割的过程。

现在就要把维塔利的这个构造，扩展到球体上。首先要声明的一点是，以下的构造是便于理解的简化版本，不是原版的叙述，难免有不严谨之处。但这不是大问题，因为我的目标是尽量让大家理解巴拿赫塔斯基悖论构造的思路和原理，所以无需在此时去追究细节。

具体怎么扩展？你大概也可以想到，因为从圆到球就是一个二维到三维的过程，而球体可以看做是无数条半径构成的，因此可以继续考虑，怎么对球的半径分类。难点在于，球体上的半径旋转方向太多了，我们可以先把问题限制在球面上，因为最终整个球就是所有不同半径的球面的组合。

所以，我们考虑这样一个问题：从球面上的某个点开始，设计一条合理的离散移动路线，经过无穷多个点，并且不会经过任何一个点两次。这个过程，与维塔利的构造中，从一条半径，通过转动不同角度，得到其他半径的过程的目的是一样的。通过这个过程，可以将球面上的点分成很多类，每一类的数量是可数无穷，然后就可以方便地重新组合了。

那么在球面上，要怎么移动呢？如果把球面想象成地球表面的话，我们可以规定移动方向就是东、南、西、北这个四个方向。这样，感觉上就可能移动到球面的全部位置，而不需要更多方向。每次移动的距离是多少？我们有一个目标是，不希望移动到同一个位置，那么利用无理数是一个好的思路。

所以，我们规定每次移动都是无理数的距离，比如东西方向移动，每次是√2的距离，南北向移动每次是√3的距离。又因为我们不希望回到原来的位置，我们规定每次移动后不能退回原先位置。比如向东之后不能立即向西移动。向南移动之后不能立即向北移动。当然，这样仍有可能回到原来的位置，比如走了一个矩形等等，所以需要硬性规定不能移动到之前到过的位置。所以，我们的行动方式是：

从任何一点出发，任意地向东、南、西、北四个方向之一，前进一个无理数的距离，但不能回到原来的位置，如此无限得进行下去。

（上图：某个点的移动路径示意图。绿色点为起始点，这条路径为“北东北西北西南”，最后的紫色点为“北向点”。图片来源：https://www.quantamagazine.org）

到这里，你可能会有疑问，是否会出现这种情况：到了某个位置后，选任何一个方向之后，都会回到之前去过的位置。这并不是不可能，但这个缺陷对我们的今天的讨论无关紧要，我们就忽略这个缺陷，假设无论怎么走，都可以无限的走下去，而不会出现走投无路的情况。

那么现在我们就从某一点出发，取四个方向，无限地走下去，把所有的可能路径组合都走一遍！把所有到过的点作为一个集合。这些点的特点是：可以用包含“东”、“南”、”西“、”北“、四个字符组成的路径来表示这个点，比“如东东南南西南”等等。这个字符串可以作为表示这个点的一个方法，稍后我们会用到这个路径表示。

不管怎样，我们得到了一组按第一个起始点所生成的点集合。这个集合有无穷多个元素，但是却是可数无穷多。这里，我也不严格证明为什么是可数无穷多，我需要表达的是，球面上还有很多点没有在这个集合中，还有很多点没有到过。

那么我们就从没有选到的点中，再选某点作为起始点，重复以上步骤，又得到一组可数无穷多的点。那么必然还会存在很多没有到过的点。

继续重复以上步骤，直到球面的每个点都被到达过，使每个点都属于某个起始点生成的集合。在这里，你可能又有疑问，怎么保证这样的操作是可以完成的？是否会出现某个时刻只剩下有限多的点没有到达，从而无法产生无穷多的点集合？我再一次无法严格证明这些问题，但也无关紧要，你可以相信以上操作可以完成。

如此一来，我们就把球面上的点分成了不可数无穷多组，每一组都有可数无穷多个点。然后，我们又要开始重新组合这些点了，组合方法非常巧妙。

我们先考察除了起始点之外的点。这些点都是通过上一个点经过某条路径所得到达的。那么不管这个路径如何，它总有最后一个移动方向。根据这个方向，我们把这些点分别叫做“东向点”，“南向点”，“西向点”，和“北向点”。

比如，如果A点的路径是“东东南南东”，最后一步是从另一个点向东移动达到的，那么A点就是东向点。如果B点路径的最后一步是向北移动，那么B点就是“北向点”等等。那么对球面上的点如此命名后，我们就得到了5大类点：起始点、东向点、南向点、西向点和北向点。那么对不同半径的球面都做这个操作，我们就把球上的点分成了这个五类。

现在把所有的东向点取出来，然后向西移动一步，考察一下，移动后到达的是哪些点呢？你会发现，回退后的点不能是西向点，因为之前规定移动是不能立即回退的。在某个西向点上，不能立即向东移动。所以从东向点回退一步，不会是西向点。但某个东向点的最后两步可以是“东东”、“南东”或“北东”。这意味着：

所有东向点向西移动后，它就覆盖了所有东向点，南向点和北向点！这还没完，起始点也应该包含其中！因为选定某个起始点之后，当然可以向东移动，得到一个东向点。从那些东向点向西移动，自然就包含全体起始点。

这样我们得到一个惊人结果：所有东向点向西移动一步之后，就得到了全体东向点，南向店和北向点和起始点！ 是不是有1变4的感觉！

那么，我们手头上就有1份东向点，2份南向点，1份西向点，2份北向点和2份起始点。要把球复制为两份的话，还需要1份东向点和一份西向点。

后面的步骤就简单了: 我们把南向点向北移动，得到全体东向点，南向店、西向点和起始点。那我们手头就有2份东向点，2份南向点，2份西向点，2份北向点和3份起始点。

这样我们就能把这些点组合成两个球，还多了一份起始点！这一份“起始点”浪费了吗？其实没有。之前对球面上的点分类时，还漏了一些点没有说明，那就是南极点和北极点。在移动时，我们需要规定，不能到达南极和北极点。因为一但到了这两个点，之后无法确定应该向哪里移动，所以需要禁止到达南极点和北极点。对球体来说，就是排除整个自转轴。

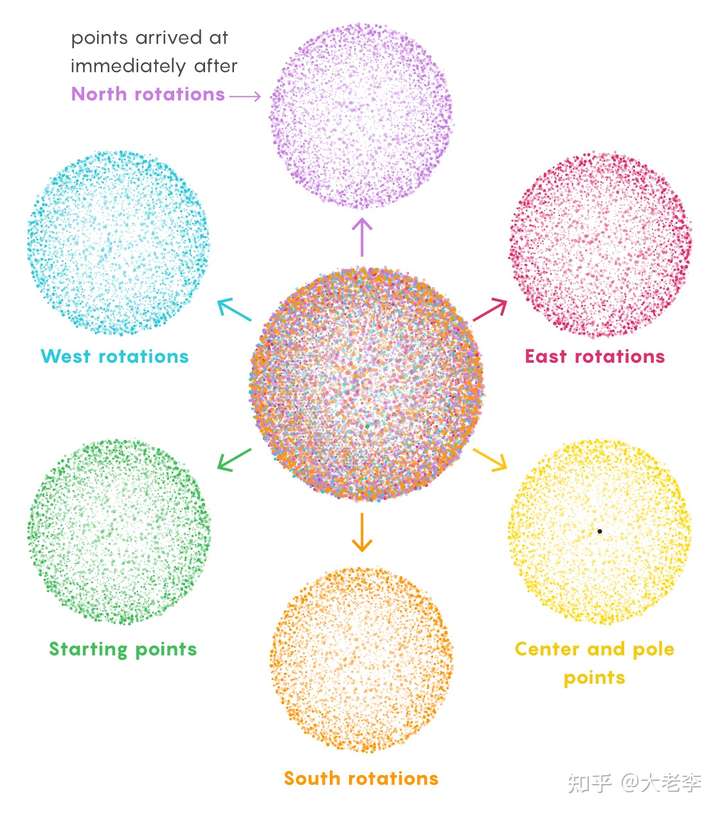（分球示意图：球上的点被分为六组：东向点、南向点、西向点、北向点、起始点、自转轴。东向点向西移动一步后，则可以复制出东向点、南向点、北向点、起始点。图片来源：https://www.quantamagazine.org）

那么既然多了一份起始点，那么这份起始点作为某个球的自转轴，那就完美了。一个球变两个球，任务完成！

那么以上，我就带大家领略了巴拿赫塔斯基悖论的基本概貌。本质上来讲，只要涉及到不可数无穷，并且允许使用选择公理，那么我们就可能遭遇这种情况。

那么数学里，是怎么能够规范这种情况，使得我们可以避免这种悖论带来的困扰？这就涉及到测度理论。我们生活中所用到的有关长度、面积和体积的概念，其实都属于“勒贝格测度”。勒贝格测度规定到了一系列有关测量的性质或公理，比如局部要小于整体；若干部分相加，应该等于整体等等，都是符合生活中的直观感觉的。

（上图：勒贝格测度的一个性质：平移不变。图片来源：维基百科）

在巴拿赫塔斯基悖论中，对球上的点所划分的若干集合，不符合勒贝格测度的定义，称其为“勒贝格不可测”，那么“体积”的概念就不适用于这个球了。

留一个思考题，上文中，我只是把东向点和南向点各回退一步。如果对西向点和北向点也回退一步，那么会得到怎样的复制结果，可以组成几个球呢？大家可以思考一下，发在评论区了。

一千年前是一家—— 一些鸽巢原理趣题

你或许已熟知这样一个原理：

当有n个笼子和n+1只鸽子，那么至少有一个笼子里有2只鸽子。

这就是“鸽巢原理”，又名"抽屉原理"或"鸽笼原理"等等。

这个原理听上去简直像废话，这是小学生都能懂的道理。但它既然能在数学里留下名字，它当然是很有用的一个原理，绝不是只能简单处理把鸽子放进笼子这样的情况。那么以下，我列举一些可以用鸽巢原理证明的有趣命题和结论。

先来一个比较简单的，生活化的例子。有若干人，在一个房间里聚会。聚会开始时互相握手认识。那么有这样一个结论：

在任何时刻，总存在两个人，与这两人握过手的人数，是相等的。

证明如下：

假设有一共有n个人，那么每个人可以握手的人数就是从0到n-1，一共有n种可能。一共有n个人，那么看上去似乎鸽巢原理用不上了呢？别急，这里面还有一个情况。如果有一个人，与其握过手的人数是n-1，那么就不应该有另一个人，与其握过手的人数是0了。同理，如果某个人一次也没有跟其他人握手，那么就不会有另一个人，与n-1个人握手。所以“0”与“n-1”，这两个数字不能共存。因此所有人的可能握手人数，其范围要么是从1到n-1，要么是从0到n-2，一共n-1种可能。

而总人数有n个人，所以必然存在2个人，他们的握手人数相等，证明完成。这个问题也经常用锦标赛来描述，结论就是，在一场锦标赛里，任何时刻总有两个人或两支队伍，他们比赛过的场次数是一样的。这是第一个例子。

再来一个比较偏数学的例子，考虑这样一个数列：

7, 77, 777, 7777，77777，777777, …

即由若干个7连写的数字构成的数列。请证明：这些数字中，至少有一个能被2027整除。

当然，你可以一个一个去试，直到找到这样一个能被2027整除的数字。但是这样很麻烦，即使用电脑编程求解，你也不知道程序需要跑多久。另外，2027是一个质数，所以你不用考虑与质因数分解相关的方法。

这里有一个使用鸽巢原理，且非常简洁的证明方法。而且，可以证明更强的结论：这个序列里不但肯定有可以被2027整除的数字，而且这个数字出现在前2027项以内。以下是证明。

首先，用反证法。假设这个数列的前2027项里，所有数字都不能被2027整除。那么这些数字除以2027，都会有余数，余数的取值范围是从1到2026，一共2026种。根据鸽巢原理，这个数列里的前2027中，必然有两个数字，它们除以2027后，所得余数相等，那么现在有意思了。

我们把这两个数字取出来，把大的那个去减去小的那个，考察相减后的数字。因为原先两个数字除以2027后余数相等，所以它们相减后，它们的差必然可以被2027整除，这一点是比较容易确认的。那么再看一下这个差值数字的形式。因为原先两个数字都是7连写构成的数字，那么它们相减后必然所得数字必然是若干个7在开头，后面有若干个0的形式：

7…70….0

这个数字可以改写为 7…7 × $10^n$ 的形式。

$10^n$ 是肯定不能被2027整除的，则那若干个“7”连写构成的整数必然能被2027整除。而那若干个“7”连写，本身就是数列的前2027项中的某一项，那么这个情况就与我们证明开始时的假设矛盾了！从而我们在证明开始时的假设不成立，这说明，这个数列的前2027项中必有一项可以被2027整除。

而这个证明也告诉我们，一般来说“鸽巢原理”给出的结论都是存在性的，而不是构造性的。这也是数学奇妙的地方之一，它可以告诉你一个东西肯定存在，但不知道在哪里。

再看一个比较生活化的例子。请证明：在任何一年，最少有4个月份，最多有5个月份，包含5个星期天。

你不信的话，可以马上看一下日历，数数有哪几个月有5个星期天。那么可以告诉你，有5个星期天的月份总是4个或5个，不过多也不会少。这个结论，可以简单得用鸽巢原理证明，大概也是唯一的方法。

因为一年365或366天，也就是52个星期多1天或2天。那么一年里至少有52个星期天，最多53个星期天（如果这一年元旦恰好是星期天）。我们要把这些星期天，分布到12个月里。因为每个月至少28天，至多31天，也就是每个月至少有4个星期天，最多5个星期天。

那么，现在就可以反证法了。如果只有3个月份有5个星期天，那么其他9个月份都是4个星期天，总共是3×5+9×4=51个星期天，就与这一天年至少有52个星期天矛盾了。而如果有6个月份有5个星期天，那么其他6个月份是4个星期天，总的星期天数量是6×5+6×4=54，这就与一天中最多53个星期天矛盾了。所以，一年中最少有4个月，最多有5个月份，包含5个星期天，证明完成！

而用鸽巢原理还能得出一些令人吃惊的有趣结论。比如，有这样一个结论：全体北京人中间，至少有两个人的头发数量相同，排除光头。这很好理解，因为人的平均头发数量是10万，不会超过15万，北京人口远超这个数量，所以北京肯定有2个人有相同的头发数量。而且北京人口实际超过2千多万，所以这个结论可以加强为：北京肯定有100个人，他们有相同数量的头发。

“鸽巢原理”可以告诉我们的一个最惊人的结论是这样一个（大概率成立的）命题：在最近1000年以内，存在这样一个历史上的人，这个人是你的父母亲的共同祖先！也就是，你的父母都是这个人的后代。

你可能会说，这怎么可能，我变成近亲结婚的后代了吗？你先别急，1000年以内，从生物学上讲已经完全不是近亲了。但是，这个结论是成立的吗？那么我们来论证一下这个结论，它可以用鸽巢原理非确定性的证明，但是大概率是成立的。

首先，如果我们从自己的父母向上追溯人口的话，你会发现每向上一代，你的祖先人数就会翻倍。你的父母有两个人；你的祖父祖母、外公外婆是4个人。你向上追溯n代，那么你就会有$2^n$个祖先。

那么我们假设每25年，有一代人的更迭。那么1000年的话，大约是40代。如果你的祖先40代，都是不同的人，那么总的人数就是 $2+4+8+....+2^{40}=2^{41}-1$ 人，大约是2.2 × $10^{12}$ ，也就是22万亿人，这个数字太吓人了！根据历史记载，最近1000年，地球上存在过的人口数量，远小于22万亿人。所以，这就说明，你的祖先这40代人，不可能都是不同的人！很可能，有某人是你父母的共同祖先。

但为什么说这不是一个100%严谨的证明呢？因为还存在这样一种可能：你父亲这一支向上的祖先，发生过很多的合并，也就是你父亲的祖先里，有很多人有共同的祖先。同样，你母亲这一支的祖先中，也有很多人有共同的祖先。这样你父母亲的祖先这两支人口，就不需要那么多人了，有可能，你父母的祖先在1000年内完全是两个没有交集的群体。但这也说明，如果以上结论对你不成立，那么这个结论就会对你的父母更大概率的成立。

这就是鸽巢原理告诉我们的一个反直觉结论。它让我想起了一些延伸的结论。既然以上结论适合你的父母，其实它也适合任何两个人。

比如，中国人有句俗语，对同姓氏的人，我们常说“五百年前是一家”。根据以上推导，这句话还真不是一句客套话，而是可以从数学上证明的。同姓氏的两个人，非常有可能在500年内，有一个共同祖先，尤其是那些不常见的姓氏。

那么有关鸽巢原理，就聊到这里。鸽巢原理虽然内容简单，但是它确实能帮我们证明一些意想不到的结论。最后，出两道有意思的，与鸽巢原理相关的思考题，供大家消遣娱乐：

史密斯夫妇，邀请4对夫妇到家里来玩。这4对夫妇中，有些人是史密斯先生的朋友，有些是史密斯太太的朋友，有些互相之间认识，有些不认识。当这4对夫妇到达史密斯夫妇的家中后，所有之前互相认识的人都握手了一下。史密斯先生发现了一个有意思的情况，他说：如果把我排除在外，剩下的人中，每个人握手的次数都是不同的。这里，有两个隐含条件是：自己不会跟自己握手，夫妻之间也当然不需要握手。现在的问题是：史密斯太太握了几次手？

这个问题听上去是不是有点不可思议，因为已知条件如此至少，怎么突然就问史密斯太太握了几次手？但是，根据鸽巢原理，确实可以唯一的确定史密斯太太的握手次数。请你来做一次侦探，推理出这个数字。

参考文档：

Click to access A%20Walk%20Through%20Combinatorics%20An%20Introduction%20to%20Enumeration%20and%20Graph%20Theory.pdf

欧拉遇到过的最难的积分：全体自然数的立方倒数和

（本文原载于我在知乎上的回答，原问题是：“你遇到过的最难的积分题目是什么？”，略修改）

这不是我遇到过的最难的积分，这是欧拉遇到过的最难的积分：

$(\frac{1}{2}\int_0^1\frac{(\ln x)^2}{1-x}dx)$

1734年，27岁的欧拉计算出全体自然数的平方的倒数和是 $(\pi^2/6)$ :

$(1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+...=\frac{\pi^2}{6})$

这个成就使欧拉一下子名声大噪，成为数学家中的社会名人。以上这个问题后来以欧拉的家乡瑞士巴塞尔命名，称为“巴塞尔问题”。

欧拉自己也很兴奋，他一鼓作气，计算了指数为偶数，直到26次方的自然数幂次倒数和的情况：

$(1+\frac{1}{2^4}+\frac{1}{3^4}+\frac{1}{4^4}+\frac{1}{5^4}+...=\frac{\pi^4}{90})$

$(1+\frac{1}{2^6}+\frac{1}{3^6}+\frac{1}{4^6}+\frac{1}{5^6}+...=\frac{\pi^6}{945})$

… $(1+\frac{1}{2^{26}}+\frac{1}{3^{26}}+\frac{1}{4^{26}}+\frac{1}{5^{26}}+...=\frac{\pi^{26}\cdot 2^{24}\cdot 76977927}{27!})$

那么问题就来了，指数为3的情况下，结果如何呢？这个问题意外地困难。欧拉一生中曾经多次挑战这个问题，找到了许多相关结果，比如奇数的3次幂的交错级数情况：

$(1-\frac{1}{3^3}+\frac{1}{5^3}-\frac{1}{7^3}+\frac{1}{9^3}-...=\frac{\pi^3}{32})$

然而欧拉始终不能对自然数立方倒数和问题找出一个“简单”的确切答案。他曾经“自然地”（因为偶数幂次都是这个形式）作出猜想，这个问题的答案应该是: $(\frac{p}{q}\pi^3)$ 的形式，其中 $(p/q)$ 是个有理数。

后来，他又找到了文章开头的那个积分式：

$(\frac{1}{2}\int_0^1\frac{(\ln x)^2}{1-x}dx)$ $(=\frac{1}{2}\int_0^1(\ln x)^2(1+x+x^2+x^3+...)dx)$ $(=\frac{1}{2}\int_0^1[\sum_{r=0}^{\infty}x^r(\ln x)^2]dx)$ $(=\frac{1}{2}\sum_{r=0}^{\infty}\frac{2}{(r+1)^3})$ $(=\sum_{k=1}^{\infty}\frac{1}{k^3})$

然而这个积分看似简单，但始终无法继续计算或化简。

1785年，在欧拉去世后2年出版的论文中，可以看到欧拉在生命中的最后岁月仍在尝试解决这个问题。欧拉写到“…迄今为止，没有任何办法写出这个级数的封闭形式…但是答案可能是这样一种形式”:

$(\sum_{k=1}^{\infty}\frac{1}{k^3}=\alpha[\ln 2]^3+\beta \frac{\pi ^2}{6}\ln 2)$

其中 $(\alpha)$ 和 $(\beta)$ 是有理数。

欧拉承认：“我用过如此多的方法寻找自然数的立方倒数和，然而所有方法均徒劳无功。以上（积分式）的方法也没有产生任何结果，所以看上去放弃（研究这个问题）是正确选择…”

近200年后，1978年，Roger Apery证明：全体自然数的立方倒数和是一个无理数。

他证明的结论并不让人吃惊，让数学家吃惊的是，对这个问题的研究居然还能产生一些进展，因为欧拉都放弃了！现在全体自然数的立方倒数和就被被称为“Apery常数”。

有人问对平方倒数和可否凑出类似的积分式？仿造欧拉的方法，很容易得到如下积分式，恰好等于全体自然数的平方倒数和：

$(\int_0^1\frac{\ln x}{x-1} dx)$

有wolframalpha为证：

这个不定积分wolfram给我的答案是：

不是常见的封闭形式，而使用了对数积分函数。2021.12.8我收到知乎用户“诱宵美9”私信，她搞出一个可以积的，全体自然数平方倒数和的积分，计算过程如下：

$(\int_{0}^{1} \frac{\mathrm{d} x}{(1+y x) \sqrt{1-x^{2}}})$

用 $(x=\sin t)$ 换元：

$({\int_{0}^{\pi / 2}} \frac{\mathrm{d} t}{1+y \sin t})$ $(=\left.\frac{2 \arctan \left(\frac{\tan \frac{t}{2}+y}{\sqrt{1-y^{2}}}\right)}{\sqrt{1-y^{2}}}\right|_{0} ^{\pi / 2})$ $(=\frac{\arccos y}{\sqrt{1-y^{2}}})$

从而有：

$(\int_{-1}^{1}\left(\int_{0}^{1} \frac{\mathrm{d} x}{(1+y x) \sqrt{1-x^{2}}}\right) \mathrm{d} y)$

$(=\int_{-1}^{1} \frac{\arccos y}{\sqrt{1-y^{2}}} \mathrm{~d} y)$

$(=-\left.\frac{1}{2} \arccos ^{2} y\right|_{-1} ^{1}=\frac{\pi^{2}}{2})$

交换积分级数顺序:

$(\int_{-1}^{1}\left(\int_{0}^{1} \frac{\mathrm{d} x}{(1+y x) \sqrt{1-x^{2}}}\right) \mathrm{d} y)$

$(=\int_{0}^{1}\left(\int_{-1}^{1} \frac{1}{(1+y x) \sqrt{1-x^{2}}} \mathrm{~d} y\right) \mathrm{d} x)$

$(=2 \int_{0}^{1} \frac{\arctan x}{x \sqrt{1-x^{2}}} \mathrm{~d} x)$

从而：

$(\sum_{n=1}^{\infty} \frac{1}{(2 n-1)^{2}}=\frac{\pi^{2}}{8})$ $(=\sum_{n=1}^{\infty} \frac{1}{n^{2}}-\sum_{n=1}^{\infty} \frac{1}{(2 n)^{2}})$ $(=\frac{3}{4} \sum_{n=1}^{\infty} \frac{1}{n^{2}})$

于是有：

$(\sum_{n=1}^{\infty} \frac{1}{n^{2}}=\frac{\pi^{2}}{6})$

牛，这个我是想不出来的！就是有点复杂，期待还有更简单形式的积分。

以下是目前有关此问题的一些进展：

首先如果把指数视为自变量，则以上级数求和已被一般化，归入黎曼Zeta函数(以下定义仅适用s>1的情况)：

$(\zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^{s}})$

对于s为偶数的情况，欧拉时代就已经解决：

$(\zeta(2 n)=\frac{(2 \pi)^{2 n}(-1)^{n+1} B_{2 n}}{2 \cdot(2 n) !})$

其中 $(B_n)$ 称为“伯努利数”，它们满足递推关系：

$(\left(\begin{array}{c} n+1 \ 1 \end{array}\right) B_{n}+\left(\begin{array}{c} n+1 \ 2 \end{array}\right) B_{n-1})$ $(+\ldots+\left(\begin{array}{c} n+1 \ n \end{array}\right) B_{1}+1=0, \forall n)$

对s为奇数的情况则所知甚少。1978年Apery证明 $(\zeta(3))$ 是无理数，仍未知其是否超越数。2001年有人证明，必然有无穷多个 $(\zeta(2k+1))$ 是无理数，且 $(\zeta(5))$ 、 $(\zeta(7))$ 、 $(\zeta(9))$ 、 $( \zeta(11))$ 中，至少有一个是无理数。

开头那个积分是欧拉算不出的，以下介绍一个欧拉遇到过的，也相当难但确实是可以算的积分：

$(\int_0^{\frac{\pi}{2}} \ln(\sin x)dx)$

不妨自己先算算看……

当代“规范”解法，先拆分：

$(\begin{aligned} I &=\int_{0}^{\pi / 2} \ln (\sin x) d x=\int_{0}^{\pi / 2} \ln \left(2 \sin \frac{x}{2} \cos \frac{x}{2}\right) d x \ &=\int_{0}^{\pi / 2}(\ln 2) d x+\int_{0}^{\pi / 2} \ln \left(\sin \frac{x}{2}\right) d x+\int_{0}^{\pi / 2} \ln \left(\cos \frac{x}{2}\right) d x \end{aligned})$

再换元，令t=x/2：

$(\begin{aligned} I &=\frac{\pi}{2} \ln 2+2 \int_{0}^{\pi / 4} \ln (\sin t) d t-2 \int_{\pi / 2}^{\pi / 4} \ln \left(\cos \left[\frac{\pi}{2}-t\right]\right) d t \ &=\frac{\pi}{2} \ln 2+2 \int_{0}^{\pi / 4} \ln (\sin t) d t+2 \int_{\pi / 4}^{\pi / 2} \ln (\sin t) d t \ &=\frac{\pi}{2} \ln 2+2 \int_{0}^{\pi / 2} \ln (\sin t) d t=\frac{\pi}{2} \ln 2+2 I \end{aligned})$

原积分形式复现，太好了，可以解出:

$(I=-\frac{\pi}{2}\ln 2)$ .

欧拉的“不规范”解法：

首先，证明这样一个等式：

$(\cos x=2\sin 2x \sin x +2\sin 4x \sin x +2\sin 6x \sin x+...)$

方法是，根据积化和差公式：

$(2\sin nx \sin x=\cos (n-1)x-\cos (n+1)x)$

所以：

$(\cos x = \cos x +(-\cos 3x + \cos 3x )+(-\cos 5x + \cos 5x )+(-\cos 7x + \cos 7x )+...)$ $(=( \cos x -\cos 3x) + (\cos 3x -\cos 5x) + (\cos 5x -\cos 7x) + ...)$ $(=2\sin 2x \sin x +2\sin 4x \sin x +2\sin 6x \sin x+...)$

再计算 $( y=\ln(\sin x))$ 的微分，当然， $(\frac{d y}{d x}=\frac{\cos x}{\sin x})$ ,代入以上公式：

$(d y=\frac{\cos x}{\sin x} d x=\frac{2 \sin 2 x \sin x+2 \sin 4 x \sin x+2 \sin 6 x \sin x+\cdots}{\sin x} d x)$ $(=2[\sin 2 x+\sin 4 x+\sin 6 x+\cdots] d x)$

再倒回去，对两边积分：

$(\begin{aligned} y &=\int d y=2 \int[\sin 2 x+\sin 4 x+\sin 6 x+\sin 8 x+\cdots] d x \ &=2\left[-\frac{1}{2} \cos 2 x-\frac{1}{4} \cos 4 x-\frac{1}{6} \cos 6 x-\frac{1}{8} \cos 8 x-\cdots\right]+C \ &=-\cos 2 x-\frac{1}{2} \cos 4 x-\frac{1}{3} \cos 6 x-\frac{1}{4} \cos 8 x-\frac{1}{5} \cos 10 x-\cdots+C \end{aligned})$

C是一个待定的常数。恰好已知当 $(x=\pi / 2)$ 时， $(y=\ln (\sin \pi /2)=0)$ ，代入上式，可得：

$(0=-\cos \pi-\frac{1}{2} \cos 2 \pi-\frac{1}{3} \cos 3 \pi-\frac{1}{4} \cos 4 \pi-\frac{1}{5} \cos 5 \pi-\cdots+C)$

那么:

$(C=-1+\frac{1}{2}-\frac{1}{3}+\frac{1}{4}-\frac{1}{5}+\cdots)$ ，恰好这个级数值是已知的(这道题大概很多课本里是作为习题的吧)，为 $(-\ln 2)$ ，所以得到：

$(\ln (\sin x)=-\ln 2-\cos 2 x-\frac{1}{2} \cos 4 x-\frac{1}{3} \cos 6 x-\frac{1}{4} \cos 8 x-\frac{1}{5} \cos 10 x-\cdots)$

然后就可以求它的积分了：

$(\begin{aligned} \int_{0}^{\pi / 2} & \ln (\sin x) d x \ &=\int_{0}^{\pi / 2}\left[-\ln 2-\cos 2 x-\frac{1}{2} \cos 4 x-\frac{1}{3} \cos 6 x-\frac{1}{4} \cos 8 x-\cdots\right] d x \ &=\left.\left((-\ln 2) x-\frac{1}{2} \sin 2 x-\frac{1}{8} \sin 4 x-\frac{1}{18} \sin 6 x-\frac{1}{32} \sin 8 x-\cdots\right)\right|_{0} ^{\pi / 2} \ &=-\frac{\pi}{2} \ln 2 \end{aligned})$

以上过程中，每一项sin都正好抵消。

欧拉的方法虽然看上去很繁复，但有一种把无穷级数玩弄于股掌之间的感觉。