这次跟大家聊聊“扭结理论”,就是研究“结”(Knot)的数学理论。数学真的是包罗万象,连打结也可以研究。
相信你小时候可能也曾想过这样的问题:画出一个结的形状,怎么判定它是一个活结?也就是拉这个结的两端,最后能还原成一直线?
这是最早的,研究扭结理论的一个动机。但数学家又发现,如果有两个开放端的话,对问题的描述不够简便,所以他们规定,数学里的结是把两个开放端连起来的。这样数学里的“结”就是一条封闭的绳环,在三维空间里缠绕构成的一个空间多边形。

(上图:这个结看上去很复杂,但是可以还原成一个环。有没有办法,简单判定一个结是否就是环?)
因为有很多扭结形状很漂亮,所以很多公司的logo就是采用扭结的图形。比如中国联通的logo,就是取自一个中国结的形状,当然也是一个很标准的数学中的扭结。

还有香港的亚洲电视台2010年前的Logo,就是一个标准的“三叶结”:
 (上图:香港的亚洲电视台2010年前的Logo,就是一个三叶结)
(上图:香港的亚洲电视台2010年前的Logo,就是一个三叶结)
那么可以想象,一个绳环所能构成的最简单形状当然就是一个圆环,这是最简单的一种结,这种形状被称为“unkot”,中文叫“平凡结”。
 (上图:动视暴雪旗下的一个游戏工作室:Treyarch的logo,很像三叶结,但我仔细看了一下之后,发现其实是平凡结。)
(上图:动视暴雪旗下的一个游戏工作室:Treyarch的logo,很像三叶结,但我仔细看了一下之后,发现其实是平凡结。)
但是显然,不是所有的绳环都能最后还原成成一个圆环,所以问题就是:给定一个结的图形,怎么判定它是不是“平凡结”?或者,更一般的问题是:给定两个结,怎么判定它们其实是同一种结?
当然,对简单的结你可以目测判定,但是对很复杂形状,目测就会失效,所以数学家希望找到合适的数学方法去研究扭结。
这里的一个难点是,同一个扭结,形状可以千变万化,但是需要忽略绝大多数变化,只关注我们需要的变化。所以,数学家需要寻找的是“不变量”,就是变化中的对象的某个不改变的属性。就像我们如果再次见到几十年没见到的朋友,也许他的外貌发生了很大的变化,但是你可能发现,他的声音,生态,举止没有变化。那么这些属性就是“不变量”,这些属性可以帮我们识别一个人。
高斯曾经想出了一个办法,可以对一个“结”用数字串表示出来。也就是当别人看到这串数字后,可以还原出你所需要的结。但是,在他的方法,同一个结确可以有多种不同的表示,也没有简单方法判定两个数字串是否表示同一个结,所以对结的分类来说并不太有用。
高斯的结的数字表示法:
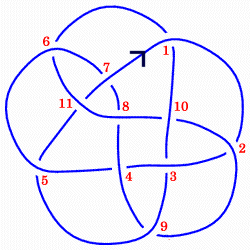
把结画在平面上,从一个结的任何一个位置开始,给定一个方向,沿线“游历”这个结。当第一次穿过某个“交叉点”时,对这个交叉点递增编号。并且规定,如果从上方穿过交叉点,编号取正,下方穿过,编号取负。那么上图的结的“高斯数字表示”就是:
1 -2 3 -4 5 6 -7 -8 4 -9 2 -10 8 11 -6 -1 10 -3 9 -5 -11 7
但此法并不总能确保还原出同样的结,因此有一种稍有变化“扩展的高斯表示”:当第二次穿过某个交叉点时,数字的正负由构成交叉点的两条线段的“手性”确定,右手手性为正,左手手性为负,则上述结的“扩展高斯表示”就是:
1 -2 3 -4 5 6 -7 -8 -4 -9 -2 -10 8 11 6 -1 -10 3 9 -5 -11 -7
那么对一个扭结来说,有什么样的不变量?你能想到的第一个属性应该就是交叉点数。一个扭结你把它放平放在桌上,通过整理,可能可以把绳与绳之间的交叉点减少若干,到一定程度后,就无法继续减少了。那么这交叉点数就是一个结的不变量。
这个交叉点数确实是一个扭结的不变量,比如平凡结,它的交叉点数就是0。而最简单的一个非平凡结,“三叶结”,它的交叉点数就是3。

(7个交叉点以内的一些结)
但可惜的是,交叉点数并不是一个很有用的扭结不变量,有两个原因:给定一个结的形状,如何判定,这个形状里的交叉点数已经不能再减少了,这没有一个确切的方法。
比如看下联通的logo,图形上一共有9个交叉点,但其中有5个交叉点,并没有画出确切的上下关系。但是你可以看到,最左边和最右边的那两个交叉点显然是可以去掉的,也就是那两个圈可以去掉。
那现在问,如果允许随意安排剩下三个交叉点的上下关系,这联通logo能还原成一个平凡结吗?你稍微看一下会发现,是可以。但是如果问,是否存在对那三个交叉点的某种安排,使得它不能还原成圆环呢?你会发现,这三个交叉点的上下关系,有8种组合,每一种都考虑一遍的话,那是相当麻烦,更不用说更复杂的结了。所以,不能简便判定一个结的最少交叉点数,是“交叉点数”作为扭结不变量的一个缺陷。
还有一个缺陷是,相同的交叉点数下,存在很多不同的扭结,而且交叉点越多,不同的扭结也越多。这也意味着交叉点数并不能很好的区分扭结,所以这是另一个缺陷。
在扭结理论历史上,有两次重大的关于扭结理论的突破。第一次是1928年,美国数学瓦德尔·亚历山大提出了一个扭结不变量,称为“亚历山大多项式”。并且他证明了,如果两个结可以互相转化,那么它们的这个特征多项式就可以互相转化。这样判定两个结是否等价就容易多了,因为多项式化简大家都会的,这要比直接看图形方便多了。所以这是第一个重大突破。亚历山大本人也对很多扭结进行了分类,给出了一个列表。
1970年代,英国数学家,约翰·康威又独立发明了一种“亚历山大多项式”的变体和另一种表示法。所以,这个多项式有时也被称为“亚历山大——康威”多项式。
但是亚历山大多项式也有一个缺陷,少数情况下,不同的结仍然会具有相同的亚历山大多项式,特别是一个结和它的镜像,必然有相同的亚历山大多项式。比如你打一个三叶结,再拿面镜子,你会看到镜子的三叶结的镜像。它们肯定有许多相同的性质,但是你把一个三叶结无论怎么变换,你也没法把它变成它的镜像,所以,从这个意义上说,三叶结和它的镜像是两种结,但是亚历山大多项式是无法区分它们的。
一个更极端和让人吃惊的例子是平凡结,平方结的亚历山大多项式是“1”,但是还有一些其他看上去相当复杂的结,它的亚历山大多项式也是1。这是亚历山大多项式的一个缺点。

(上图:以上这个名为”Pretzel knot (-3 5 7)”的结的亚历山大多项式也是”1“,它有很多有趣且出人意料的特点)
扭结理论的再一次重大突破,是在1984年。新西兰数学家沃恩·琼斯(Vaughan Jones,1952年12月31日-2020年9月6日),发现了另一个扭结不变量,现在成为“琼斯多项式”。这个多项式在区分和表达扭结的能力上比“亚历山大多项”式更好。

更为奇妙的是,在琼斯发表了琼斯多项式之后不久,美国物理学家爱德华·威腾(Edward Witten,)发现了琼斯多项式与量子场论之间有着奇妙的联系。爱德华·威腾的名字,相信很多读者是很熟悉的,他是弦理论和量子场论的顶尖专家,并且是“M理论”的创立者。而M理论是目前一种比较有希望的“大统一理论”。
爱德华·威腾发现琼斯多项式可以运用到量子场论里,这个发现是如此让人遐想连篇:难道宇宙的微观结构中存在一个个扭结?
不管怎样,琼斯和威腾的发现也是如此重要,使得二人双双在1990年,获得了数学界的最高荣誉之一:菲尔兹奖。而这有两个不寻常之处,一个是威腾是目前仅有的以物理学家身份获得菲尔兹奖的人。琼斯则被认为是以最短的论文,获得菲尔兹奖的人。琼斯的关于琼斯多项式的论文一共就8页,而且其中有4页是一些扭结的多项式数据表格和引用之类。论文实际内容也就4页。仅凭4页的论文获得菲尔兹奖也是绝无仅有的例子。
那么以上我们简单聊了扭结两种多项式表示的不变量:亚历山大多项式和琼斯多项式。下面我再简单聊聊扭结的另外一种有趣的性质:扭结的分解和加法组合。
这里先得定义结的组合,也经常简称为加法。其实可以想象结的加法就是设法把两个结连接起来。把结连起来的方法有很多种,所以我们需要精确定义,避免产生歧义。那么数学中结的加法是大概这样的:

(结的“加法”:把两个结尽量放平在桌面上,互不重合。在两个结之间,找某个比较靠近的部分,画一个矩形。要求矩形两对边分别在两个结上,矩形本身不覆盖任何结。在矩形两对边处,各剪一刀,得到4个开放端,上面的两个开放端连在一起,下面的两个开放端连在一起,就得到了一个新的结。这个结称为原先两个结的”连接和“(connected sum)。 图片来源:维基百科)
此加法定义马上带来的一个有趣问题是:两个结的加法结果是否是唯一的?以上定义只说了选择靠近的两部分进行连接,所以连接的位置是可以任意选择的。那么连接不同的部分,所得的结是否仍然一样?还好数学家证明了,在严格的定义下,这种加法的结果是唯一的。
结的加法有了,那么它的逆操作就是结的分解。有了组合和分解操作后,一下子就可以考虑很多有意思的问题。结的加法有没有交换律和结合律?答案是肯定,你可以自己做些实验验证。
还有一个“显然”的结论是:一个结加上平凡结,所得结果是其本身。那么是否存在两个或多个非平凡结,它们相加后变为平凡结呢?可能有人会有这种想法:一个结加上它镜子里的图像,两者就会互相“抵消”,最后变成一个环呢。但答案有点意外,是否定的。这是1949年,数学家舒伯特(Schubert)证明的:一个非平凡结,无论再给它加上怎样的结,也没法对它“抵消”,最后变成一个环。
再说两个有关结的加法的有趣例子:三叶结的相加。三叶结是最简单的非平凡三叶结。三叶结加三叶结所得图形被称为“granny knot”,我叫它“老奶奶结”。

三叶结+三叶结的镜像所得结,称为“suqare knot”,中文叫“平结”。这个“平结”知道的人应该更多些,因为这是很实用的一种捆扎方式,急救时也经常用平结来固定绷带。而这个老奶奶结和平结也是攀岩运动中,非常实用的两种结的类型,我相信玩攀岩的和海员,应该对这两种结很熟悉。
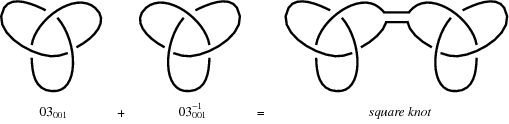
平结和老奶奶结具有相同的亚历山大多项式,但琼斯多项式可以区分它们。
再看看结的分解,就更有意思了。结的分解就是结加法的逆运算。显然,存在这样一些结,对它们没法分解了。如果继续分解,也只能分出平凡结,比如三叶结。那么对这种没法分解的解,数学家给它起了个名字(也许你猜到了):“素结”(Prime Knot)。
这里,我们可以把结想象成整数,平凡结想象成数字1,结的分解想象成质因数分解,那么“素结”就像素数,所以命名为“素结”。
这就马上带来一个有意思的问题:结的世界中,有“唯一因子分解定理”吗?也就是,当一个结不是素结,而是一个“合结”的时候,把这个“合结”分解为若干素结的组合,那么分解结果是唯一的吗?
答案是肯定的,1949年,还是数学家舒伯特证明了(把结的方向定向之后),合结的分解结果是唯一的。
那有没有一个办法判定一个结是素结呢?答案如同质因数分解,目前没有一个简单的方法或者快捷算法,判定一个结是否是素结。所以,给定一个结,如何对其“素结分解”也就是一个比较困难的问题。由此,甚至有人设想可以用“结”,构造一个非对称加密体系。
好了,以上就是我给大家讲的扭结理论的一些入门知识,主要是亚历山大多项式和琼斯多项式,它们都是“扭结不变量”,而琼斯多项式还与物理中的量子场论有关系,并且琼斯因此获得了菲尔兹奖。后半段讲了扭结的加法和分解操作,扭结在这方面的很多性质与整数的质因子分解很像。扭结理论的起因是非常简单,就是来源于人们希望对“结”进行分类和整理,但衍生出的话题确实非常之多,甚至于物理学中最前沿的理论联系起来,不得不令人叹为观止。
参考链接:
https://www.britannica.com/science/knot-theory
https://www.maa.org/press/periodicals/convergence/unreasonable-effectiveness-of-knot-theory
https://knotinfo.math.indiana.edu/descriptions/gauss_notation.html
https://mathworld.wolfram.com/KnotSum.html
https://mathworld.wolfram.com/GrannyKnot.html
https://mathworld.wolfram.com/SquareKnot.html