这篇知乎上的文章中的后半部分，我们领略了数学家维塔利的一个构造，这个构造可以把一个圆变成两个圆。
回顾一下维塔利的构造要点。首先，这种构造之所以存在，是基于无穷集合的基数理论。无穷集合中，集合的真子集可以与自身建立一一对应，这是这种构造存在的基本理论依据。但是，对不可数集合，要建立某种貌似离散的切割和组合操作，完成子集到自身的一一对应，难度还是很大的。从维塔利的构造中，我们看到了这个构造的基本理念：
把一个不可数集合分割成无数个子集，每个子集都是可数集。可数集中，比较容易建立子集到整体的一一对关系，所以最后的重组工作就比较容易，难点在于分割的过程。
现在就要把维塔利的这个构造，扩展到球体上。首先要声明的一点是，以下的构造是便于理解的简化版本，不是原版的叙述，难免有不严谨之处。但这不是大问题，因为我的目标是尽量让大家理解巴拿赫塔斯基悖论构造的思路和原理，所以无需在此时去追究细节。
具体怎么扩展？你大概也可以想到，因为从圆到球就是一个二维到三维的过程，而球体可以看做是无数条半径构成的，因此可以继续考虑，怎么对球的半径分类。难点在于，球体上的半径旋转方向太多了，我们可以先把问题限制在球面上，因为最终整个球就是所有不同半径的球面的组合。
所以，我们考虑这样一个问题：从球面上的某个点开始，设计一条合理的离散移动路线，经过无穷多个点，并且不会经过任何一个点两次。这个过程，与维塔利的构造中，从一条半径，通过转动不同角度，得到其他半径的过程的目的是一样的。通过这个过程，可以将球面上的点分成很多类，每一类的数量是可数无穷，然后就可以方便地重新组合了。
那么在球面上，要怎么移动呢？如果把球面想象成地球表面的话，我们可以规定移动方向就是东、南、西、北这个四个方向。这样，感觉上就可能移动到球面的全部位置，而不需要更多方向。每次移动的距离是多少？我们有一个目标是，不希望移动到同一个位置，那么利用无理数是一个好的思路。
所以，我们规定每次移动都是无理数的距离，比如东西方向移动，每次是√2的距离，南北向移动每次是√3的距离。又因为我们不希望回到原来的位置，我们规定每次移动后不能退回原先位置。比如向东之后不能立即向西移动。向南移动之后不能立即向北移动。当然，这样仍有可能回到原来的位置，比如走了一个矩形等等，所以需要硬性规定不能移动到之前到过的位置。所以，我们的行动方式是：
从任何一点出发，任意地向东、南、西、北四个方向之一，前进一个无理数的距离，但不能回到原来的位置，如此无限得进行下去。
（上图：某个点的移动路径示意图。绿色点为起始点，这条路径为“北东北西北西南”，最后的紫色点为“北向点”。图片来源：https://www.quantamagazine.org）
到这里，你可能会有疑问，是否会出现这种情况：到了某个位置后，选任何一个方向之后，都会回到之前去过的位置。这并不是不可能，但这个缺陷对我们的今天的讨论无关紧要，我们就忽略这个缺陷，假设无论怎么走，都可以无限的走下去，而不会出现走投无路的情况。
那么现在我们就从某一点出发，取四个方向，无限地走下去，把所有的可能路径组合都走一遍！把所有到过的点作为一个集合。这些点的特点是：可以用包含“东”、“南”、”西“、”北“、四个字符组成的路径来表示这个点，比“如东东南南西南”等等。这个字符串可以作为表示这个点的一个方法，稍后我们会用到这个路径表示。
不管怎样，我们得到了一组按第一个起始点所生成的点集合。这个集合有无穷多个元素，但是却是可数无穷多。这里，我也不严格证明为什么是可数无穷多，我需要表达的是，球面上还有很多点没有在这个集合中，还有很多点没有到过。
那么我们就从没有选到的点中，再选某点作为起始点，重复以上步骤，又得到一组可数无穷多的点。那么必然还会存在很多没有到过的点。
继续重复以上步骤，直到球面的每个点都被到达过，使每个点都属于某个起始点生成的集合。在这里，你可能又有疑问，怎么保证这样的操作是可以完成的？是否会出现某个时刻只剩下有限多的点没有到达，从而无法产生无穷多的点集合？我再一次无法严格证明这些问题，但也无关紧要，你可以相信以上操作可以完成。
如此一来，我们就把球面上的点分成了不可数无穷多组，每一组都有可数无穷多个点。然后，我们又要开始重新组合这些点了，组合方法非常巧妙。
我们先考察除了起始点之外的点。这些点都是通过上一个点经过某条路径所得到达的。那么不管这个路径如何，它总有最后一个移动方向。根据这个方向，我们把这些点分别叫做“东向点”，“南向点”，“西向点”，和“北向点”。
比如，如果A点的路径是“东东南南东”，最后一步是从另一个点向东移动达到的，那么A点就是东向点。如果B点路径的最后一步是向北移动，那么B点就是“北向点”等等。那么对球面上的点如此命名后，我们就得到了5大类点：起始点、东向点、南向点、西向点和北向点。那么对不同半径的球面都做这个操作，我们就把球上的点分成了这个五类。
现在把所有的东向点取出来，然后向西移动一步，考察一下，移动后到达的是哪些点呢？你会发现，回退后的点不能是西向点，因为之前规定移动是不能立即回退的。在某个西向点上，不能立即向东移动。所以从东向点回退一步，不会是西向点。但某个东向点的最后两步可以是“东东”、“南东”或“北东”。这意味着：
所有东向点向西移动后，它就覆盖了所有东向点，南向点和北向点！这还没完，起始点也应该包含其中！因为选定某个起始点之后，当然可以向东移动，得到一个东向点。从那些东向点向西移动，自然就包含全体起始点。
这样我们得到一个惊人结果：所有东向点向西移动一步之后，就得到了全体东向点，南向店和北向点和起始点！ 是不是有1变4的感觉！
那么，我们手头上就有1份东向点，2份南向点，1份西向点，2份北向点和2份起始点。要把球复制为两份的话，还需要1份东向点和一份西向点。
后面的步骤就简单了: 我们把南向点向北移动，得到全体东向点，南向店、西向点和起始点。那我们手头就有2份东向点，2份南向点，2份西向点，2份北向点和3份起始点。
这样我们就能把这些点组合成两个球，还多了一份起始点！这一份“起始点”浪费了吗？其实没有。之前对球面上的点分类时，还漏了一些点没有说明，那就是南极点和北极点。在移动时，我们需要规定，不能到达南极和北极点。因为一但到了这两个点，之后无法确定应该向哪里移动，所以需要禁止到达南极点和北极点。对球体来说，就是排除整个自转轴。
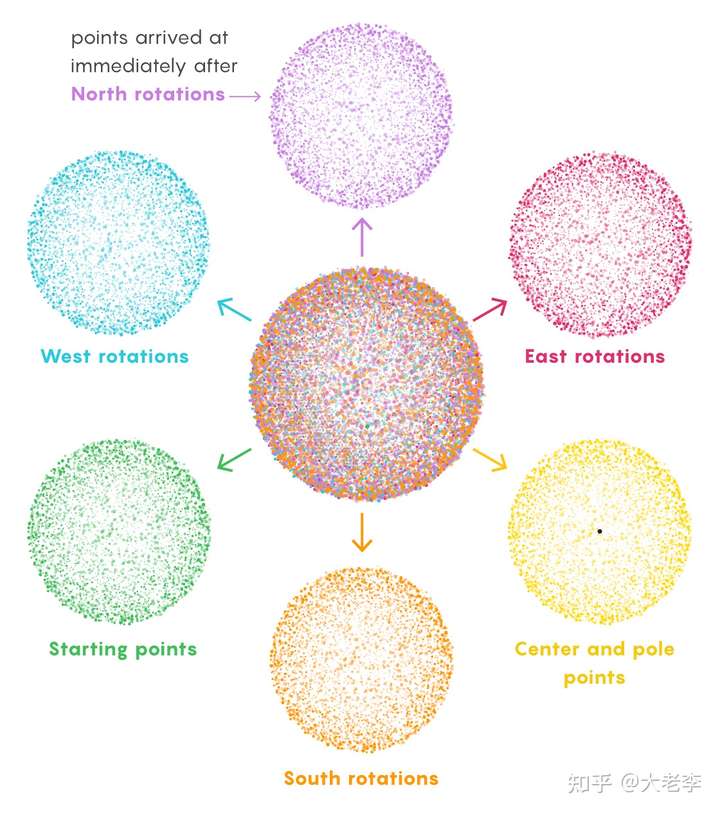（分球示意图：球上的点被分为六组：东向点、南向点、西向点、北向点、起始点、自转轴。东向点向西移动一步后，则可以复制出东向点、南向点、北向点、起始点。图片来源：https://www.quantamagazine.org）
那么既然多了一份起始点，那么这份起始点作为某个球的自转轴，那就完美了。一个球变两个球，任务完成！
那么以上，我就带大家领略了巴拿赫塔斯基悖论的基本概貌。本质上来讲，只要涉及到不可数无穷，并且允许使用选择公理，那么我们就可能遭遇这种情况。
那么数学里，是怎么能够规范这种情况，使得我们可以避免这种悖论带来的困扰？这就涉及到测度理论。我们生活中所用到的有关长度、面积和体积的概念，其实都属于“勒贝格测度”。勒贝格测度规定到了一系列有关测量的性质或公理，比如局部要小于整体；若干部分相加，应该等于整体等等，都是符合生活中的直观感觉的。
（上图：勒贝格测度的一个性质：平移不变。图片来源：维基百科）
在巴拿赫塔斯基悖论中，对球上的点所划分的若干集合，不符合勒贝格测度的定义，称其为“勒贝格不可测”，那么“体积”的概念就不适用于这个球了。
留一个思考题，上文中，我只是把东向点和南向点各回退一步。如果对西向点和北向点也回退一步，那么会得到怎样的复制结果，可以组成几个球呢？大家可以思考一下，发在评论区了。
大老李聊数学 